如何判断并找出函数的拐点？

函数的拐点：探索数学曲线中的转折点

在数学的广阔天地里，函数作为描述现实世界变化规律的基本工具，其图像形态千变万化，蕴含着丰富的信息。其中，拐点作为函数图像上的一个特殊点，不仅标志着函数性态的显著变化，也是微积分学、最优化理论等领域中不可忽视的重要概念。本文将带您深入探索函数的拐点，从定义出发，逐步揭示其几何意义、判定方法以及在实际应用中的价值。

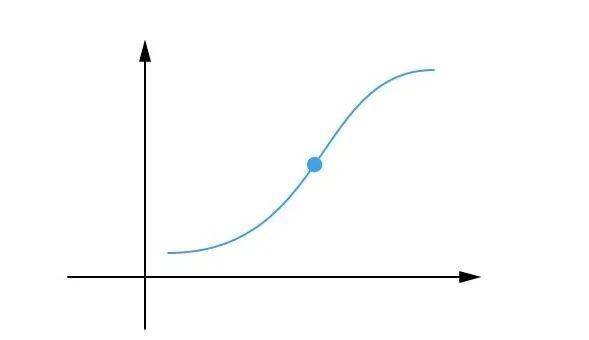
一、拐点的定义

在数学上，拐点（Point of Inflection）通常定义为函数图像上二阶导数变号的点，或者说，是函数图像上切线斜率（即一阶导数）的变化率发生改变的点。换句话说，当函数在某点处由凹变凸或由凸变凹时，该点即为拐点。需要注意的是，拐点并不意味着函数值本身达到极大或极小，而是指函数图像弯曲方向的改变。

为了更直观地理解，我们可以想象一条平滑的道路，在某个位置，道路由上坡突然变为下坡（或相反），这个转折点就是道路的“拐点”。类似地，在函数图像上，这样的转折点就是函数的拐点。

二、拐点的几何意义

1. 弯曲方向的变化：最直接地，拐点标志着函数图像弯曲方向的变化。在拐点之前，函数图像可能呈现上凸（即开口向下的抛物线形状），而在拐点之后则可能变为下凸（开口向上）。反之亦然。

2. 一阶导数单调性的转变：由于拐点处二阶导数变号，这也意味着函数的一阶导数（即斜率）在此处可能达到极值或改变单调性。虽然一阶导数的极值点不一定是拐点，但拐点的存在往往伴随着一阶导数性质的显著变化。

3. 视觉上的显著点：在图形绘制或数据分析中，拐点往往是最吸引眼球的点之一。它们能够迅速抓住观察者的注意力，揭示数据或函数变化的关键时刻。

三、拐点的判定方法

1. 二阶导数测试：最常用的拐点判定方法是检查函数的二阶导数。若在某点处，函数的二阶导数由正变负或由负变正，则该点即为拐点。这是因为二阶导数反映了函数曲线的凹凸性，其变号意味着凹凸性的改变。

2. 一阶导数分析法：虽然一阶导数不直接用于判断拐点，但通过观察一阶导数的变化也可以间接推断拐点的存在。例如，当一阶导数由递增变为递减（或相反）时，很可能伴随着拐点的出现。然而，这种方法需要结合其他信息（如二阶导数）来准确判断。

3. 图形观察法：对于简单的函数，直接观察其图像也是判断拐点的一种有效方法。通过肉眼观察函数图像在哪些位置发生了弯曲方向的改变，即可大致确定拐点的位置。但这种方法依赖于图形的清晰度和观察者的经验，可能不够精确。

四、拐点的应用实例

1. 经济学中的供需分析：在经济学中，需求曲线和供给曲线常常出现拐点。这些拐点代表着市场状态的转变点，如从供不应求转变为供过于求，或相反。了解这些拐点有助于政策制定者预测市场趋势，制定合适的经济政策。

2. 物理学中的运动学问题：在物理学中，研究物体的运动轨迹时，加速度的拐点往往对应着物体运动状态的显著变化。例如，在竖直上抛运动中，物体的加速度在到达最高点时由向下变为向上（虽然加速度大小不变，但方向改变），这一点就是加速度的拐点，也是物体运动状态的转折点。

3. 工程设计中的结构优化：在工程设计中，如桥梁、建筑等的结构设计往往需要考虑到材料的受力情况。通过分析结构在不同位置处的应力分布和变化趋势，可以找到应力的拐点，从而确定结构的关键部位，进行针对性的加固或优化。

4. 生物学中的生长曲线：在生物学中，生物体的生长曲线往往呈现出S型，其中包含了多个拐点。这些拐点代表了生物体生长速率的显著变化，如从缓慢生长进入快速增长阶段，或从快速增长逐渐趋于稳定。研究这些拐点有助于理解生物体的生长规律和影响因素。

五、结语

综上所述，函数的拐点作为函数图像上的一个特殊点，不仅具有深刻的数学意义，还在多个领域展现出广泛的应用价值。通过掌握拐点的定义、几何意义、判定方法以及实际应用，我们可以更加全面地理解函数的性质和行为规律，为解决实际问题提供有力的数学工具。在未来的学习和研究中，不妨多留意身边的拐点现象，用数学的眼光去探索和发现更多的奥秘。