立方体的体积公式是什么？

立方体，作为三维空间中最基本的几何体之一，其体积计算是几何学中的基础内容。在日常生活中，无论是建筑设计、工程计算还是科学实验，立方体的体积公式都扮演着至关重要的角色。本文将从立方体的定义出发，深入探讨立方体的体积公式及其应用，旨在帮助读者更好地理解这一几何概念。

首先，我们需要明确立方体的定义。立方体，又称正方体，是一个六个面都是正方形的特殊多面体。它的每个面都是完全相同的正方形，且任意两个相邻面都相互垂直。立方体的这一特性使得它在几何学中具有独特的地位。由于立方体的所有棱长都相等，我们通常用字母a来表示这一公共棱长。

接下来，我们进入本文的核心内容——立方体的体积公式。立方体的体积公式是：V = a³，其中V代表体积，a代表立方体的棱长。这个公式简洁明了，却蕴含着深刻的几何意义。它告诉我们，立方体的体积与其棱长的三次方成正比。换句话说，如果立方体的棱长增加一倍，其体积将增加八倍。这一特性使得立方体的体积计算在实际应用中尤为重要。

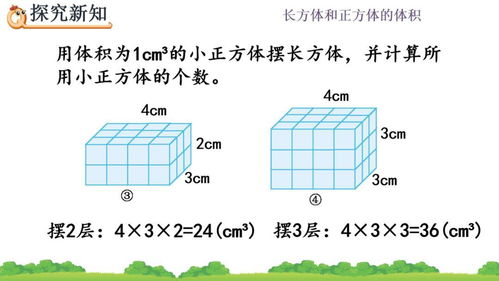
为了更直观地理解立方体的体积公式，我们可以通过一个简单的例子来进行说明。假设有一个边长为2厘米的立方体，我们可以利用公式V = a³来计算其体积。将a=2代入公式，得到V = 2³ = 8立方厘米。这意味着，这个立方体的体积是8立方厘米。通过这个例子，我们可以看到，立方体的体积公式在实际应用中是非常方便和有效的。

立方体的体积公式不仅在数学和物理学中有广泛应用，还在工程学、建筑学等领域发挥着重要作用。在工程设计中，工程师经常需要计算各种形状和尺寸的物体的体积，以便进行材料采购、成本估算和结构设计。立方体作为最基本的几何体之一，其体积公式在这些计算中起到了基础性的作用。在建筑学中，立方体的体积公式同样具有重要意义。建筑师在设计建筑物时，需要考虑建筑物的空间布局、使用功能和美观性。通过计算立方体的体积，建筑师可以更好地规划建筑物的内部空间，确保建筑物既实用又美观。

此外，立方体的体积公式还与一些有趣的数学问题相关联。例如，著名的魔方问题就与立方体的体积密切相关。魔方是一个由多个小立方体组成的立体拼图玩具，通过旋转和移动这些小立方体，玩家可以还原魔方的原始状态。在解决魔方问题的过程中，玩家需要运用立方体的体积公式来计算魔方的总体积以及每个小立方体的体积，从而更好地理解魔方的结构和解法。

除了上述应用外，立方体的体积公式还与一些重要的数学概念相联系。例如，立方体的体积与表面积之间存在一定的关系。立方体的表面积公式为S = 6a²，其中S代表表面积，a代表棱长。通过比较立方体的体积公式和表面积公式，我们可以发现，立方体的体积与其表面积的六分之一的立方根成正比。这一关系在几何学中具有一定的理论价值。

此外，立方体的体积公式还与立方根的概念紧密相关。在数学中，立方根是指一个数的三次方根，即找到一个数，使得这个数的三次方等于给定的数。立方体的体积公式实际上就是一个求立方根的过程：给定立方体的体积V，我们可以通过求V的立方根来得到立方体的棱长a。这一过程在数学运算和实际问题解决中都具有重要意义。

在探讨立方体的体积公式时，我们还需要注意一些常见的误区。例如，有些人可能会将立方体的体积公式与长方体的体积公式混淆。长方体的体积公式为V = lwh，其中l、w、h分别代表长方体的长、宽和高。虽然长方体和立方体都是多面体，但它们的体积计算公式是不同的。立方体作为长方体的一个特例（长、宽、高都相等），其体积公式可以看作是长方体体积公式的一种简化形式。因此，在计算立方体的体积时，我们必须明确使用立方体的体积公式，以避免计算错误。

总之，立方体的体积公式是几何学中的基础内容之一，具有广泛的应用价值和重要的理论意义。通过深入理解立方体的体积公式及其应用，我们可以更好地掌握几何学的基本知识，提高解决实际问题的能力。无论是科学研究、工程设计还是日常生活，立方体的体积公式都发挥着不可替代的作用。因此，我们应该重视这一基础知识的学习和应用，不断提高自己的几何素养和数学能力。